Our Experiment
In our experiment, we examine the influence of time dilation on the wavelengths of transmission signals received by the International Space Station (ISS).



Time dilation, a key concept in Einstein's theories of relativity, describes how time can appear to 'slow down' or 'speed up' depending on certain conditions. There are two primary types of time dilation: gravitational time dilation and velocity (or kinematic) time dilation.
Gravitational Time Dilation: According to Einstein's theory of General Relativity, gravity can distort the fabric of spacetime. This results in gravitational time dilation, where time moves slower in stronger gravitational fields. So, a clock closer to a massive object (like a planet or a star) will run slower than a clock that is located further away.
Velocity Time Dilation: This form of time dilation arises from Einstein 's Special Theory of Relativity. It occurs due to differences in relative velocity between two observers. If one observer is moving relative to another observer, the moving observer 's clock will seem to run slower. This effect becomes particularly significant as the relative velocity approaches the speed of light.
How is this relevant to the ISS?
In the context of the International Space Station (ISS), both types of time dilation are relevant. The ISS is moving at high speeds relative to an observer on Earth (velocity time dilation), and it's also further from the center of the Earth and thus experiences less gravitational pull (gravitational time dilation).
Application
To find the total time dilation effect on the ISS, we need to combine both types of time dilation. This is done by adding the individual effects. It's important to note that because the effects are very small, they don't simply add linearly. Instead, we have to use the principles of Einstein's relativity to properly combine them, giving a more accurate estimation of the overall time dilation experienced aboard the ISS. The equations are as such:
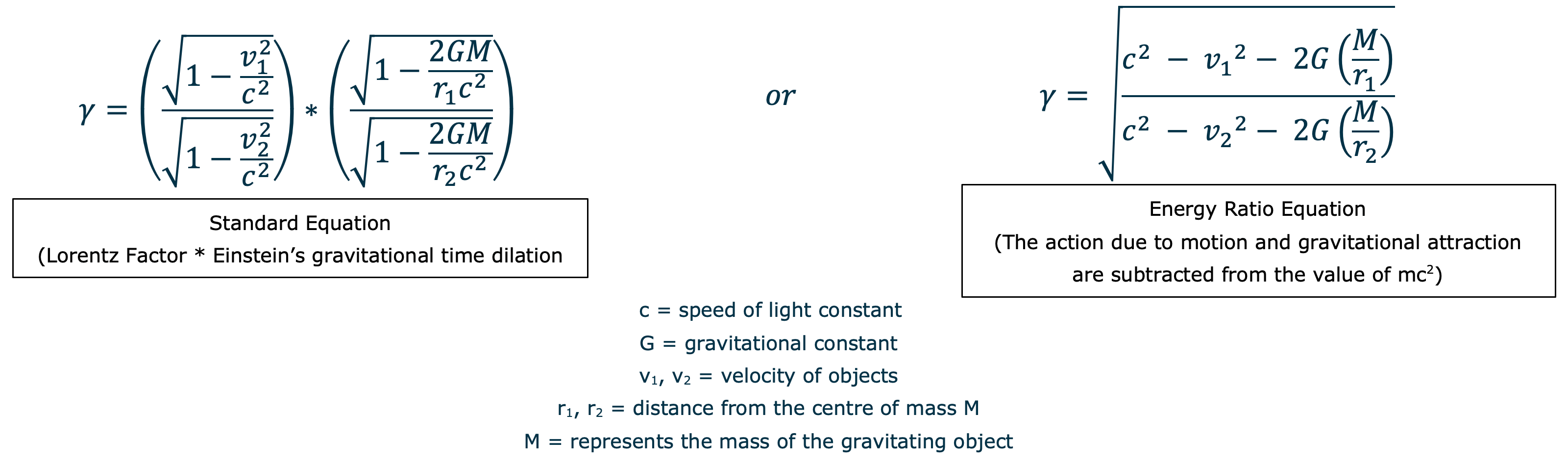
To calculate the total time dilation experienced by the ISS, we simply substitute the values we've obtained into one of the relevant equations.
Finding the Wavelength
Once the time dilation effect has been calculated, it can be applied to the wavelength of the uplink transmission to the ISS. This is done by multiplying the time dilation factor by the original wavelength. The wavelength of a wave is directly proportional to its period (and inversely proportional to its frequency), so if time appears to be 'stretched' due to time dilation, so too will the wavelength. The equation to calculate the wavelength recieved by the ISS is as follows:
Time Dilation (γ) x Original Uplink Wavelength (λ) = Wavelength Recieved